先日、京都大学で原子核物理の実験をなさっている、関口仁子先生の三体核力の講義を受けて、感銘を受けたとともに、帰り道に気さくに話しかけてくださっただけでなく激励の言葉も頂き、すっかり先生に陶酔してしまったのでブログで宣伝することで皆様に関口先生の取り組みを知っていただきたいと思って書かせていただいています。内容が高校、大学の教養物理をかっ飛ばすものなので数式による説明は途中で消えてしまいますがどうぞお付き合いください。物理がわからない人でも理解できる内容になっているので是非ついてきてください！週一ペースで上げられるよう頑張ります！
目次
古典力学で語る自然現象
cofeebreak:対称性
初回講義とレポートの感想
次の講義
古典力学（高校で学ぶ力学のことです。）で語る自然現象とは、三次元*の一様*等方*空間上で一様な時間*の下で点粒子*（物体を大局的に見た時に見える）が互いの相互作用*のみで振る舞うものである。
〔＊三次元:ここではユークリッド3次元空間のことを表す。
＊一様: 空間上での任意の並進移動に対する普遍性を持つ。
＊等方:空間上での任意の回転移動に対する普遍性を持つ。
以上2つは宇宙原理と呼ばれる。
＊一様な時間:非相対論である。つまり時間の流れは常に一定で、すべての事象に対して普遍性を持つ。
＊点粒子:物体は膨大な数の原子により構成されているが、その一つ一つについて考えていては日が暮れてしまう。それゆえどうにか簡単にできないかと考えたところ、遠くの人が見た物体の様子を考えるとどうもうまくいく。ここでは数式でそのことについて表現する。
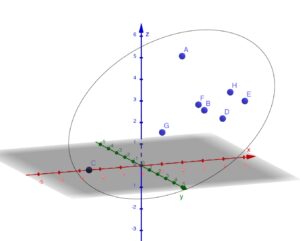
1〜nまでのn個の粒子で構成される一体系（法則を適用する対象）に関しての運動方程式は（運動方程式が慣性質量（粒子が力を受けた時に現れる、加速度の変化のしにくさの粒子固有の性質）・加速度＝その粒子にかかる力なのは実証実験でわかる。例えば、地表付近で物体を投げた時、放物運動（微小で見ると連続する運動）になるのは初期位置と初期速度を決めることで次の瞬間の位置と速度が順々に決まっていくからである。しかし、初期位置と速度を決めても次の瞬間の位置が決まるだけで速度は決まらない。つまり、他の粒子からの相互作用と外力が変えるのは速度の微小変化、加速度で、力を感じた時の感じにくさを示すのが慣性質量であるから、F＝maとなる。）以下のようになる。Fabが表すのは、bがaに及ぼす力である。
m1×a1 = F12+F13+F14……….+f1外
m2×a2 = F21+F23+F24……….+f2外
:
:
mN×aN = FN1+FN2+FN3…………+fN外
２粒子間の相互作用について考えると、相互作用力は2粒子の相対位置に比例し、実証実験から作用反作用の法則の存在は自明である。よってF12 = – F21 // rであるから、
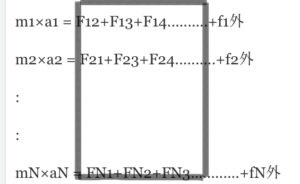
黒枠内、つまりNこの粒子の全内力の合計は0になる。
つまり全てを足し合わせると、Σmi×Σai=Σfi外とまとめることができる。
ここで、左辺にΣmiをかけて割ってみると、左辺＝M（N個の粒子の全質量）×（Σmi×Σai）/ Σmiとなる。（Σmi×Σai）/ Σmiは一体系の加重平均をとっているので、一体系の重心の加速度を示すこととなる。つまり、一体系の運動方程式はM×A＝全外力となる。この式が意味することはどんなに複雑で多くの粒子で構成されている物体でも、質点が系の全質量を持ち、系が受けた全外力を質点が受け、運動しているとみなすことができる。古典物理学での議論の対象となるのは質点の運動である。
＊相互作用:粒子同士が互いに影響を及ぼしあうこと。自然界には以下4つの相互作用がある。重力相互作用、電磁相互作用、強い相互作用、弱い相互作用である。古典物理学では、強い相互作用、弱い相互作用については測定精度の範囲外のことなので無視である。
重力相互作用を感じる粒子の基本性質を重力質量、電磁相互作用を感じる粒子の基本性質を電荷と呼ぶ。〕
世の中には様々な対称性が存在します。目で見えるものも目に見えないものも多く存在する、対称性の定義とは何でしょうか。それは任意の変換に対する普遍性を持つことです。
回転対称は、任意の回転に対する普遍性、つまり回転しても回転する前の状態と区別がつかないことを意味します。二次関数のグラフは、軸に対して線対称ですよね、今回はその証明をしてみましょう。証明を行うときに何から手をつければいいか分からない時は目的を明確にするといいです。今回は、y=x^2が符号の変換普遍性を持つことから、y＝ax^2+bx+cも符号による変換普遍性を示すことで対称性を示せると考えます。符号による普遍性を示したいときに、厄介なのが奇関数の存在です。こういうときに便利なのは、もちろんみんな大好き平方完成です。平方完成を行うと、y=a(x+b/2a)^2-(b^2-4ac)/4aになります。x＋b/2a=-（X＋b/2a）の変換に対し、y＝Yの普遍性を持ちます。この時、(x＋ X)/2=-b/2a , (y+Y)/2=yより2次関数はx=-b/2aに対し線対称であることは自明です。
基本的に、グラフの対称性を示したいときは、符号変換普遍性に注目すれば問題なく証明できます。
一次元運動
一次元運動とは、1つの座標軸上でしか運動できないような、束縛運動のことである。別に、その座標軸はxでなくても良い。物体の様子を語るには、物体の位置、速度、加速度を知り必要がある。以下に以上についての式と導出方法を述べた。
dx/dt=v
dv/dt=a
この二式が成り立つ理由を説明できるまで咀嚼解釈することが物理学理解の第一歩である。
距離が速度×時間であることは誰でも知っている。つまりx＝vtである
d(v^2/2)=adx
投稿者 : 女子学院高等学校
