こんにちは。お茶の水女子大学附属高校2年田邊美悠です。
今回は虹が見える仕組みを数学で考察していきます。
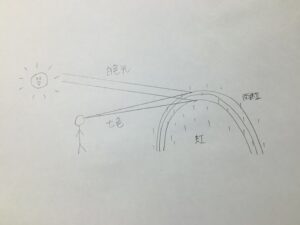
【虹の仕組み🌈】自然界に見える虹は太陽の光が雨粒に差し込み、雨粒の中で反射、屈折し、7色に分光されてその光が目に届いて虹としてみることができる。という仕組みです。下図を参照
【スネルの法則🌈】
空気に対する水の屈折率nは入射角をα、屈折角をβとすると
sinα/sinβ=n
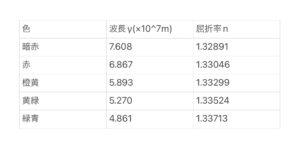
が成り立ちます。この値nはα、βの大きさに関係なく一定で、屈折率の値は色によって異なり波長の短い光ほど屈折率は大きくなります。
【本題🌈】
雨粒の中を通る光線の道筋を作図していきます。
⚠︎空気中の雨粒は球(作図時は円)として考える。
⚠︎屈折率はn=4/3とする。
⚠︎作図に用いるのはコンパスと定規のみで定規は線を引くために使う。
【作図1🌈】
「説明」
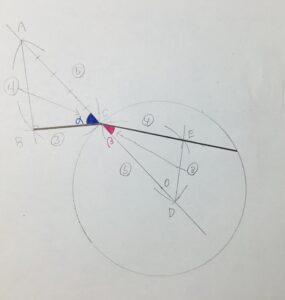
この作図では直角三角形のひ3:4:5の比を利用して考察しています。黒い太線が光線の道筋となっています。
正弦定理より、
a/sinA=b/sinB
4/sinA=3/sinB
sinA/sinB=3/4
となり、スネルの法則が成立することを利用しています。
「作図方法」
①円の中心を通る線を引く
②適当な長さで比の5に当たる部分を作図
③合同な三角形をβ側にも作図
【作図2🌈】
「説明」
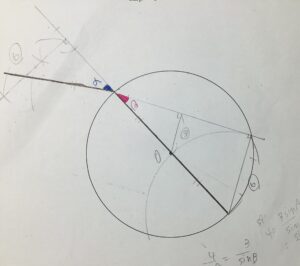
この作図では三角形の相似と、直径が半径の二倍であることを利用しています。
「作図方法」
①円の中心を通る直線を引く
②α側に三角形を作図する、但し比が6の辺は円の半径にあたる長さにする
③4/6に当たる点と①の直線を結ぶ
【作図3🌈】
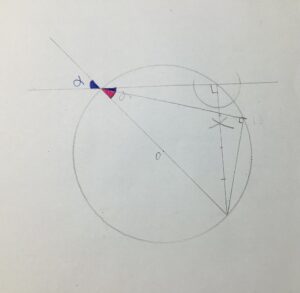
「説明」
円周角の定理を利用しています。
「作図方法」
①円の中心を通る直線を作図
②①で結んだ直線を√2とする直線三角形を円内に作図
ここで対角によりαの角が2つできる
③辺を4等分する
④下から3つ目の点を円に移す
【感想、コメント】
今回は身近な自然現象を数学で考察してみました。普段授業で習っている数学の技能が様々なところで生かされていると実感しました。また、数学の定理を受動的に学びがちなので定義を思い出してアウトプットするのはとても深い学びになると思いました。他にも作図方法がありそうなので探してみたいです。
投稿者 : お茶の水女子大学附属高等学校